【三角関数】サイン、コサイン、タンジェントは役に立つんだから!【超シンプルに解説】
三角関数のサイン、コサイン、タンジェントを勉強して何の役に立つの?
日常生活で役立つの?
この質問に回答します。
三角関数を知らないとできない仕事もありますが、自分の仕事に関係なかったら、「やっぱり全員がやる必要ないじゃん」となりますよね。
実は、三角関数は日常の意外なところで役立ちます。
この記事は2分でさらっと読めます。読んでおくと、どこかで役に立つかも。
目次
ソーラーパネルに利用される三角関数・サイン

まず、ソーラーパネルの設置方法で、三角関数を知らないとエネルギーをロスしてしまうお話から。
ソーラーパネルは、太陽光を真正面から受け取れる角度に傾けて設置すると、もっとも太陽光を利用できます。
下図のように、緯度の関係で、地球のどの場所に設置するかでソーラーパネルを傾ける角度が異なります。
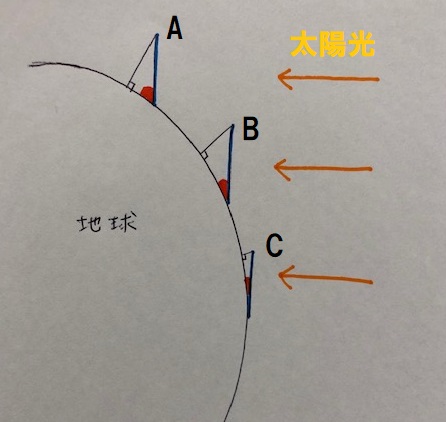
パネルが太陽光に対して垂直になるように設置したときの、傾斜角度(上図赤色)がポイントになります。
傾斜角度は緯度が高くなるほど、大きくなっていますね。
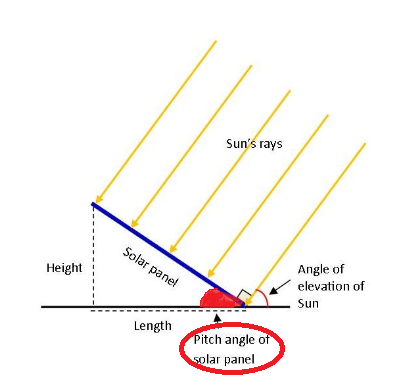
この角度を求めるときに、三角関数のサインを使います。
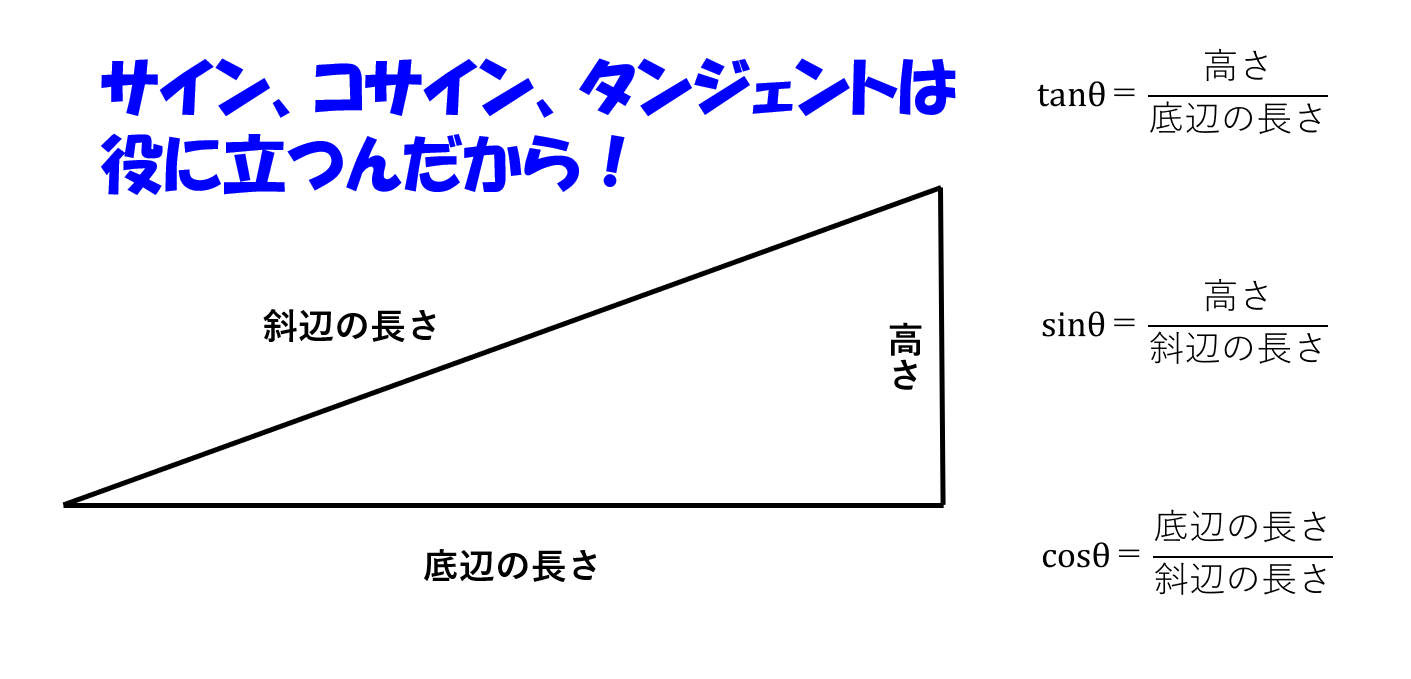
✔サインの公式は次のとおり。
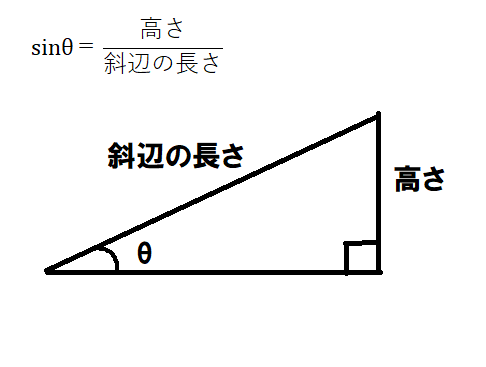
傾斜角度をαにすると、

となりますね。
もし求めたsinの値が0.5の場合は、傾斜角=30°となります。
三角関数の変換方法はこちら→三角関数の変換
スキー場での三角関数・サイン

傾斜30°のスキー場で、500m滑ったとします。
この時、どれくらいの高さから滑り降りたのか調べるのに、サインが使えます。
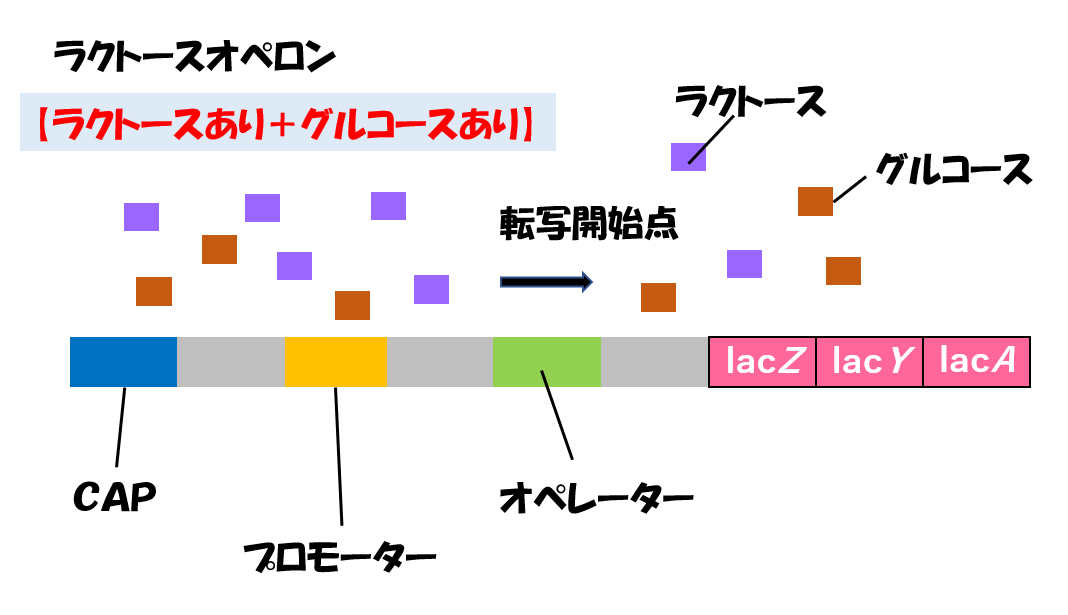
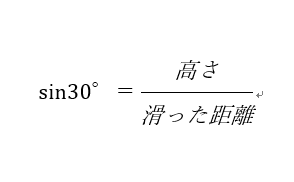
sin30°=0.5ですので、もし500m滑り降りた場合は、
高さ=0.5×500=250mとなります。
伊能忠孝が使った三角関数・コサイン

日本地図を作ったことで有名な伊能忠敬も、距離の計測に三角関数を使っていました。

伊能忠敬は、象限儀という器具で傾斜角をはかっていました。

出典:大阪市立科学館(http://www.sci-museum.kita.osaka.jp/~kazu/siryo-/shogen/Lshogen.html)
距離の計測で利用したのが三角関数のコサインです。
✔コサインの公式は次のとおり。
実際の距離を求めるには、
距離=cosθ×斜面の距離となります。
災害保険の請求に役立つ三角関数・タンジェント

意外なときに役立つことがあります。
たとえば、地震などで自宅が傾いてしまったとします。
保険会社と交渉する材料として、傾斜角度を求める際にも三角関数が役立ちます。
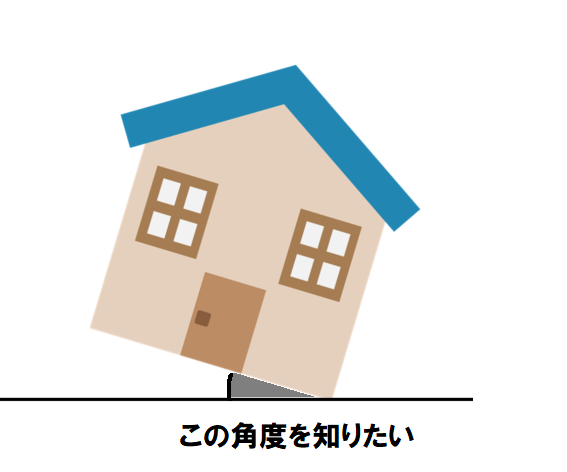
ここでは三角関数のタンジェントを使います。
下図のように①と②の長さがわかれば、タンジェントの公式を使って傾斜角度を求められます。
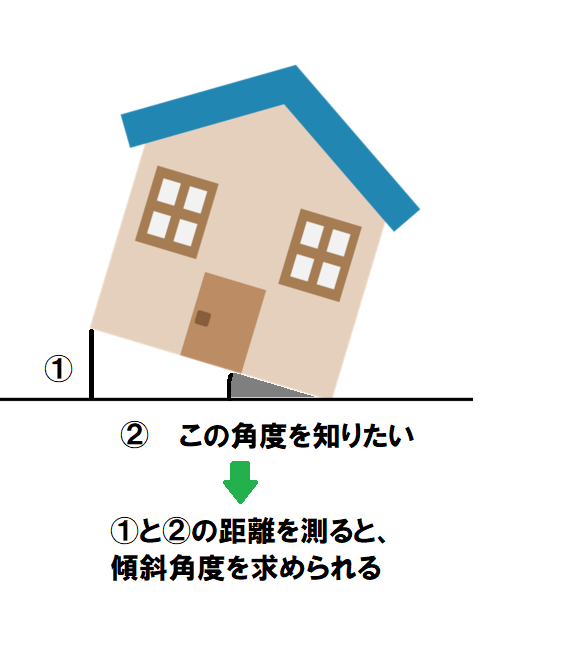
✔タンジェントの公式は次のとおり。
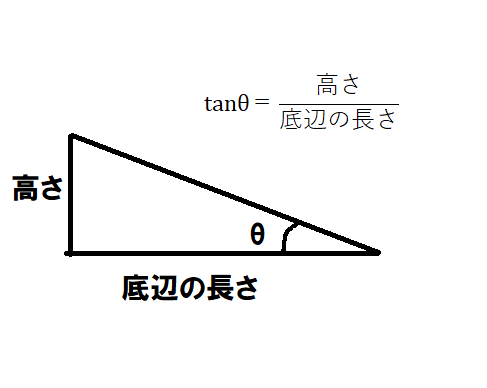
実際に、家の傾きを計測した方のお話は、こちらのツイートで知りました。
僕は文系大卒・金融機関勤務でしたが、3.11の時三角関数は役に立ちました。地震で家が傾いたので、五円玉垂らして家の壁の垂直からの乖離距離を測り(これと糸の長さでtan の値が出ます)、高校の教科書で三角関数表を見て傾きの角度を知りました。それで損保会社との話に備えることができましたです。
— takashi (@ramtakun) January 5, 2019
体のゆがみも三角関数でチェック!

人間の身体は左右対称のようで、ゆがんでいると言われますね。
右足と左足の長さが違うという方もいるのではないでしょうか。
その場合、短い足の骨盤が下のように下がっている可能性が考えられます。
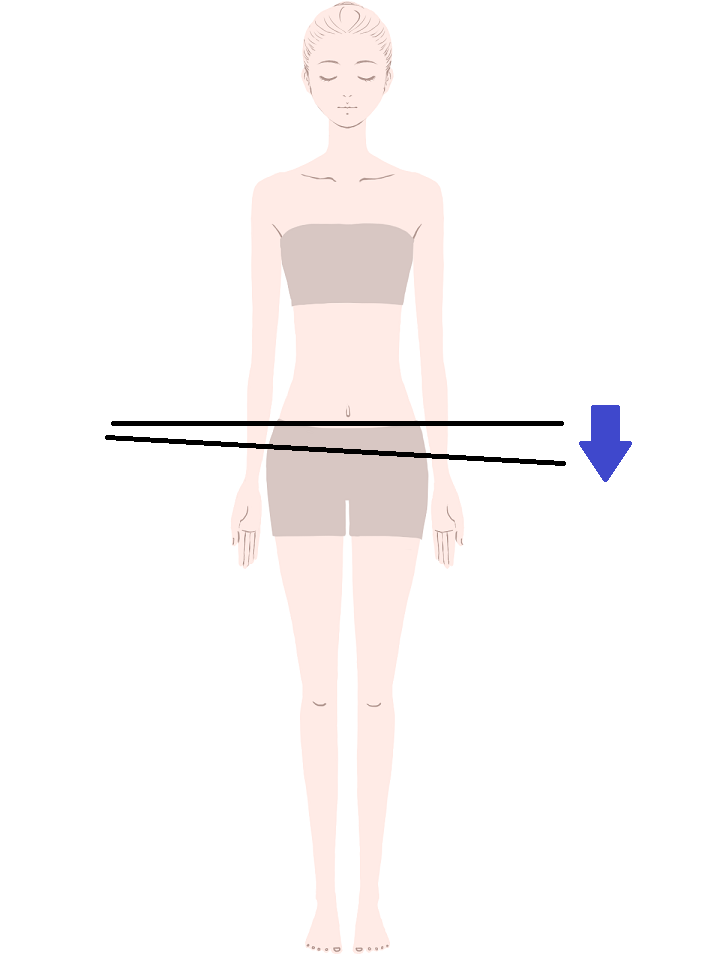
一体、どれくらい下がっているのかを調べるときにも、三角関数が役立ちます。
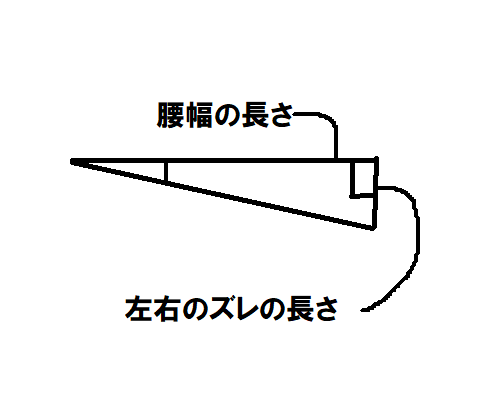
ここで使うのはタンジェント。

(左右のズレの長さ)÷(腰幅の長さ)=tanθ
tanθ=0.25であれば、片方が14°下がっていることがわかります。
三角関数の変換方法はこちら→三角関数の変換
もし体のゆがみに悩んでいて、ストレッチや整体などで改善効果を可視化したい方は、三角関数を利用されてはいかがでしょうか。
tanθの値が、施術を受けて半年後に小さくなっていたら、ゆがみが改善されているということです。
整体院が、ビフォー&アフターを示すときの営業ツールとしても使えますね。
日常生活における三角関数、探せばもっとあります。
「三角関数を学んで何の役に立つの?」という疑問は解消されたでしょうか?