息子の算数、なんでそうなる?|息子の算数成長記録(日々更新)

昨年読んで目から無数の鱗が落ちた谷口先生のこちらの本▼
読んだ直後のレビューはこちらに書きました。
この本を読んでから、
あーどうしてそこをこうするの!?
というイライラ・苛立ちに無縁になりましたよ!
まったく、どうしてそこで間違えるの?
と子供の学習を見てイライラしちゃうそこのあなた!!
読むと、子どもの「間違い」に対するイライラから解放されるどころか、間違いを分析したり考えたりするのが楽しくなりますよ。
前置きはここまでにしておいて、今回は『子どもの算数、なんでそうなる?』を読んでから、私が息子の算数の取り組みをみて、不思議だったこと・分析したこと・発見したことを記録しました。
随時更新していきます。
目次
息子の算数、なんでそうなる?-我が家の記録-
たし算すべきところでかけ算をしてしまうパターン
これは何度かありました。今でも集中力を欠くと間違えることがあります。
例 93×99の筆算
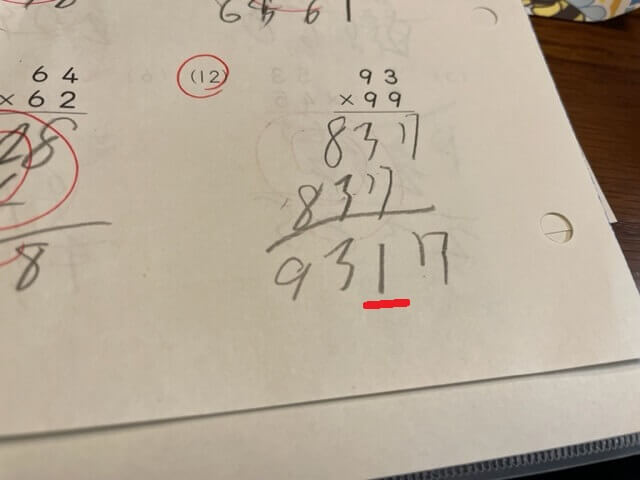
上記写真で93×99のかけ算。
「93×9=837」は合っていますが、「837+8370」と足すところで間違えています。
「837+8370=9207」なのに、「9317」と、なぜか十の位で「1」が登場しています。
息子の思考の謎解きをした結果、十の位のたし算で「3+7」とすべきところを「3×7」とかけ算しています。それなのに次の百の位の計算では「8+3+(繰り上がりの2)=13」を導いているのですよね。
例 59×59の筆算
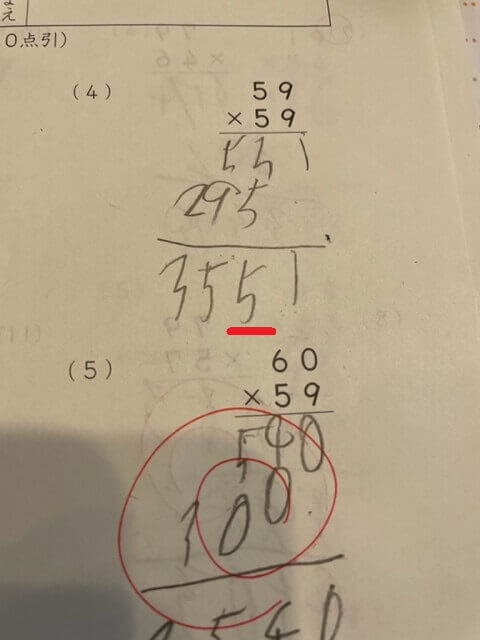
これも例①ととても似たパターンです。
「59×9」、「59×5」は合っていますが、「531+2950」と足すところで間違えています。
この例でも十の位のたし算で「3+5」をするところで「3×5」をしているのがわかります。それなのに次の百の位の計算では「5+9+(繰り上がりの1)=15」を導いています。
上記の間違いパターンを分析すると、筆算で足すべきところでかけ算をしてしまう部分に理解のあいまいさがあるのがわかりますが、
その一方で、繰り上がりのたし算、ある程度の暗算はできています。
つまり、理解のあやふやなところと、理解できている/習得できているところが混在していることがわかります。
答えは不正解ですが、理解できているのが大部分で、一部あやふやなところがあるに過ぎない、まだ過渡的な理解の状態にあることがわかりました。
こういった誤りを分析していると、下記の例でも、どこで間違えたのかすぐにわかるようになりました。

「9+2」をすべきところで「9×2」をして、その後は正しいプロセスで計算を完了しています。
息子の場合、たし算するところで突然かけ算の思考が登場しています。これを息子の思考の癖の1つととらえてからは、こういったミスが減っていくかどうかに注目することで、彼の中での理解の進度を図れるようになりました。
かけ算すべきところでたし算をしてしまうパターン
たし算をするところでかけ算をしてしまう間違いがあれば、その逆もありました。
例 73×30

73×30=300としています。
ひとつ前の「34×20」は合っていますが、「73×30」は間違えています。
どうやら、73×3=210 30×30=90 210+90=300 としているようです。
こう分析すると、子どもなりに考えていたのだな‥‥と感心さえしてしまいました。
次の「85×40」では、正解に近いやり方で340を導いていますが、「0」が足りません。
このような間違いを見ると、「×10」の時に、あとで「0」をつければよいと知らない子どもにとっては、「×10」は混乱しやすいことがわかりますし、息子も完全な理解にいたる途中経過であることがわかります。
息子には「×40」は「×4×10」と考えるとよいよ、と伝えました。
例 902×30

これは途中経過の「902×30」のときに「9×3」ではなく「9+3」をしています。
慣れてくると、間違いのパターンは限定されていて、出現する場所が異なるだけということもわかってきました。
下記もかけ算するところでたし算している例ですが、その前までの問題は合っているので、過渡的な理解の状態にあることがわかりました。
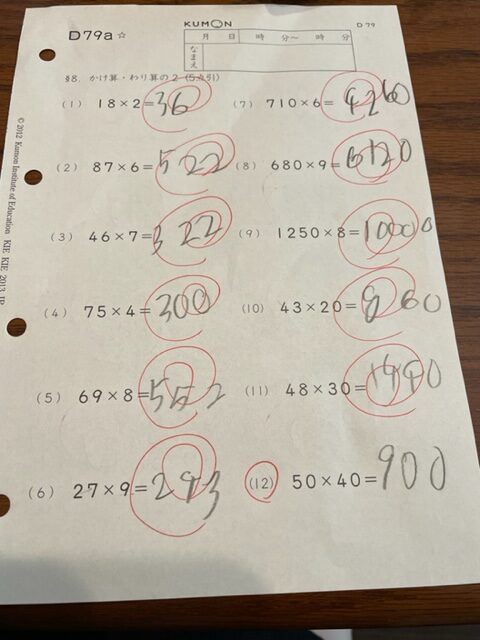
「680×9」が解けるのに、「50×40」で間違えるのは大人からすると不思議ですが、シンプルな数字の方が子どもの理解を揺さぶるものがあるかもしれません。
間違えたプロセスを分析できなかった謎
毎日見ていると、息子の間違いパターンや癖がわかってきますが、謎解きできなかった間違いもあります。
2桁以上のわり算

息子は2桁以上の商でも途中経過を書かずにやることが多いです。
上記で、「1285÷31」の答えは「41 余り14」ですが、「41」ではなく「49」を導くことが結構ありました。
これは今でも謎です。
31×4をして、128-124=4。次は45÷31のプロセスとなり、「1」が出てくると思いきや、毎回必ず「9」が登場するのです。
わり算をした答えの1の位が「1」となる問題で、「9」と回答する間違いは他にも何度かありました。
これも(暗算では)何度も間違えた問題でした▼

しかし、途中経過を書いてもらうと間違えないので、頭の中で処理しているときの間違いポイントは謎なままです。
二桁以上のわり算に慣れてからは、すんなりできることが増えました。

最も間違えたこの問題もあっさり!
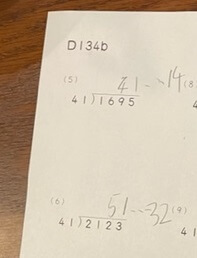
「息子の算数、なんでそうなる?」の記録は今後も続きます。
谷口先生の「子どもの算数、なんでそうなる?」はおすすめです。
こちらの記事もおすすめ