【中学入試問題】算数の旅人算で思い知る自分のオワコンぶり

思考トレーニングのために、この本を読んでいます。

子供がいなかったら、おそらく手に取らなかった本でしょう。逃げ切りを考えたはずです。
しかし私には5歳の子供がいます。この事実からはどうやったって逃げられません。
人生の大半を、「深く考えずに」生きてきてしまった私ですが、せめて、今からでも「考える」ことを習慣にしたい――という思いから、この本の入試問題に取り組んでいます。
そしたら、大きなショックが。
解説を読んでも理解できない問題に遭遇しました。
その時のツイートがこちらです。
今読んでいる2冊の本にでてくる中学入試問題。
解答を見てもわからない、解説のある一文が理解できないものがあり、自分に絶望しました。思っていた以上に論理的思考が出来ていないようです。カムフラージュしてきた綻びに今気づけたのはよかったのかも😔
子供には私のようになって欲しくない😔
— あゆみ・3Dプリンタ📚生き抜く子供を育てたい (@AyumiSato_3D) December 2, 2019
こんな方に向けて書いています
お子さんが中学受験をする予定の親御さん
つるかめ算、旅人算をやらずに方程式をやればいいと思っている人
子どもが勉強でつまづくポイントがわからない親御さん
この記事を読んだ大人が、「えー、こんな問題もわからないの?」という反応であることを願います。
目次
【中学入試問題】旅人算で思い知る自分のオワコンぶり
私が解説を読んでもすぐに理解できなかったのは、下記の問題です。
兄は学校へ、弟は幼稚園へ行くのに、兄弟同時に家を出ました。兄は分速40m、弟は分速30mで歩き、兄の方が弟よりも7分長く歩いて学校につきました。兄の歩いた距離は弟の歩いた距離よりも360m長かったそうです。兄は学校まで何分かかりましたか。
(東海中過去問)
解答を読んでも、私はすぐにわかりませんでした。
以下、前半は私の思考プロセスをお見せし、後半で解説します。
ぜひご自分で3分ほど考えてみてください。
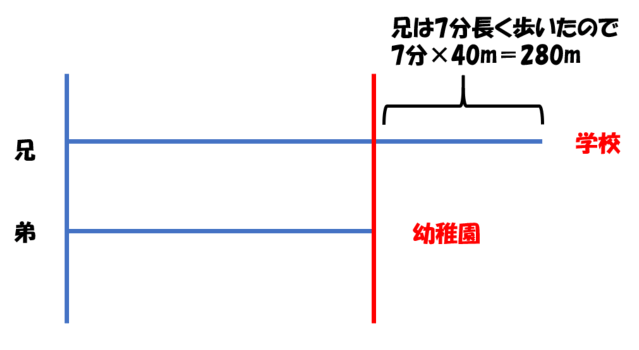
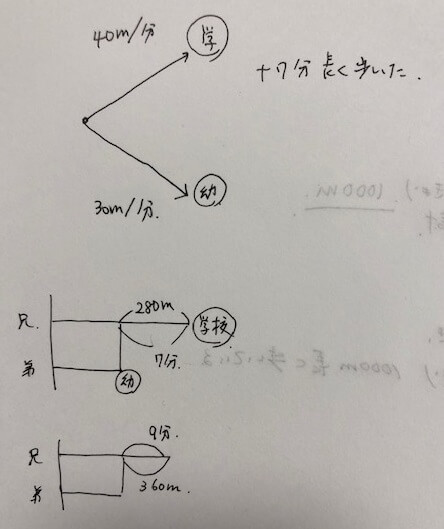
まず、私が考えたときに書いたのがこの2つの図です。
[word_balloon id=”1″ position=”L” size=”M” balloon=”talk” name_position=”under_avatar” radius=”true” avatar_border=”true” avatar_shadow=”true” balloon_shadow=”true”]自力で解答できた方は、下の1つ目の図を見て、あれ?と思うはずです。[/word_balloon]
「兄は分速40m、弟は分速30mで歩き、兄の方が弟よりも7分長く歩いて学校につきました」の記述より、兄が7分で歩いた距離は280mだと求めました。
これはすぐにわかりますよね。
次に「兄の歩いた距離は弟の歩いた距離よりも360m長かった」の記述から、次の図を書きました。
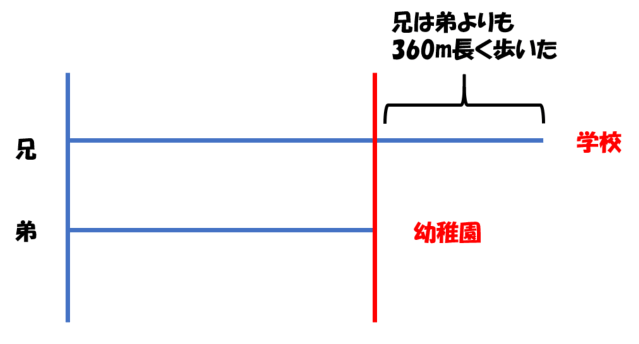
ここまで考えて、わたしは混乱しました。
280mと360mと、2つの距離が不一致なのはなぜだかわかりませんでした。
1つ目の図を見ると、「兄の方が弟よりも7分長く歩いて学校につきました」の記述を見て、兄が7分余計に歩く前の時点で、兄と弟は同じ距離を歩いていると私が思い込んでいたことがわかります。
兄が7分長く歩き始める時点で、2人の歩いた距離に「差」があることを、私は想定できなかったのです。
さらにショックなことに、解説を読んでも、すぐにわかりませんでした。
正しく図解すると、次のようになります。

図で、★までの距離が、兄と弟が同じ時間に歩いた距離となります。
分速が違うので、同じ時間に歩いた距離は当然のことながら、違います(私は気づけず)。
兄は★からさらに7分余計に歩いていますので、7分で歩いた距離は280m。
私は、7分余計に歩いた起点と、兄が弟より360m長く歩いた起点を、同じはずだと思い込んでいたため、解説を読んでもすぐにわかりませんでした。
弟が幼稚園についた時点で、二人の歩いた距離が違うことに気づけていれば、上記の図を書けたはずです。
ここまで理解できれば、あとは簡単です。
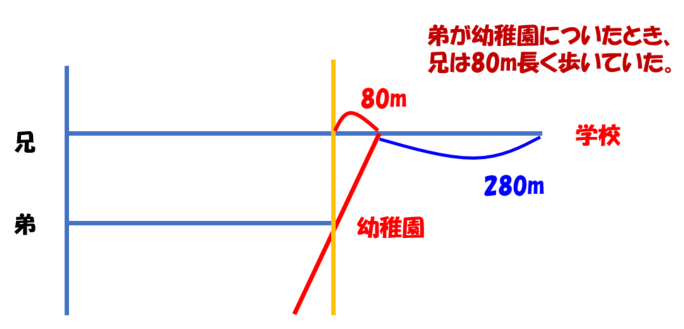
360m-280mより、弟が幼稚園についたとき、兄は80mすでに長く歩いていたことがわかります。
兄の分速=40m
弟の分速=30m
より、2人は1分歩くごとに10mの差が開いていきますので、80mの差を生むのにかかった時間は、80m÷10m/分=8分となります。
したがって、8分+7分=15分。
兄が学校に到着するまでにかかった時間は、15分となります。
私が解説を読んでもすぐに理解できなかった理由

分速が違うのだから、同じ時間に歩く距離が当然違うという当たり前の事実に考えが及ばなかったのが理由です。
一言でいえば、思い込みを外せませんでした。
1つ目の図で、おかしさに気づけていないどころか、時間と距離を一緒にした図に矛盾があることに気づけませんでした。
「兄は分速40m、弟は分速30mで歩き、兄の方が弟よりも7分長く歩いて学校につきました」の記載では、前半と後半を分けて考える必要がありました。
前半の「兄は分速40m、弟は分速30mで歩き」でまず、2人の歩く距離の差が開いていくことをイメージしたうえで、
後半の「兄の方が弟よりも7分長く歩いて」に着目すべきところ、後半にばかり気をとられて、分速の違いを無視した図を書いていましたね。
280mと360mの差に何らかのヒントがあるとわかっていても、どちらの図がおかしいのか、わかりませんでした。
問題が間違っているんじゃないの?と疑うことすらしており、私の脳のオワコンぶりがうかがえます。
子どもの成長に合わせて学びなおす覚悟を決める

最近、自分に絶望することが多いのですが、今回も絶望しました。
私は人生の大半を、「考える」ことをせずに過ごしてきてしまいました。
今、中学入試問題に取り組んでいると、早く解説を見て、楽になりたくてうずうずするんですよね。
その度に、パッとぺージをめくって、解答をさらっと読んで、解放パターンを覚えていた自分の姿がフラッシュバックします。
思えば、大学の勉強も、大学受験も、すべてこのやり方で乗り切ってきました。
だから、脳が終わっていても、あまり驚くべき事実ではありません。
私はおそらく今、人生で初めて、とことん考えようとしています。
子どもの成長に合わせて、小学校の算数レベルから、脳を鍛えなおしていきます。
いろいろな本を無料で読みたい方にはKindle unlimitedがおすすめです。
Kindle unlimitedなら初月無料で30日間読み放題です♪
こちらの記事もおすすめ