【中学受験算数】分数の割り算で逆数をかけるのはなぜ？【イメージ重視で説明してみた】
分数の割り算で、なぜ逆数をかけるのか答えられますか？
この問いは、「中学受験は算数で決まる！」の冒頭で突き付けられた質問です。
紙とペンをもって、5分ほど考えてみましたが、わかりませんでした。
今回は、本をヒントに、小学生にどうやって分数の割り算を教えるか？を考えてみます。
問題は4題あります。
[word_balloon id=”1″ position=”L” size=”M” balloon=”talk” name_position=”under_avatar” radius=”true” avatar_border=”true” avatar_shadow=”true” balloon_shadow=”true”]数式は本をヒントにしていますが、図解する考え方と、後半の3問目、4問目は、あれこれ考えているうちに私が思いついたものです。[/word_balloon]
本にも「何通りもの説明の方法があります」と書かれているとおり、考え方はたくさんあります。
本文を見る前に、ぜひ次の問題で、分数の割り算では、なぜ逆数をかけるのか？考えてみてください！
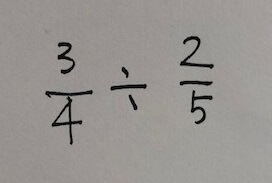
目次
【中学受験算数】分数の割り算で、逆数をかけるのはなぜ？
第１問目
次の問題を考えてみます。
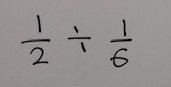
分数の割り算を求めるとき、なぜ逆数をかけるのか、数式で説明すると次のようになります。
分子、分母に同じものをかけても問題ないので、同じものをかけてみます。すると、逆数をかけていたのと同じだね、と納得させるのが狙い。
数式を使えば、ほかのパターンも納得してもらいやすいですが、数式だけで終わらせず、視覚的に理解してもらうため、レゴブロックを使ってみます。
1/2÷1/6は、レゴブロックを使うと、わかりやすくなりますね。
1/2の中には1/6がいくつあるだろう？と考えると、写真から3個とすぐにイメージできます。
ブロックで示してあげながら、数式を見せてあげると、わかりやすいかなと思いました。
紙に書いてもわかりやすいと思います。
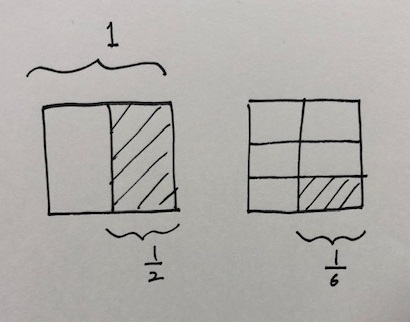
分数の概念は、数式だけだとイメージしにくいので、ブロックやピザの絵を使って説明してあげるとイメージしやすいですね。
第２問目
別の問題も考えてみます。
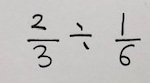
これも先ほどと同様に数式を使って説明すると、次のとおりです。
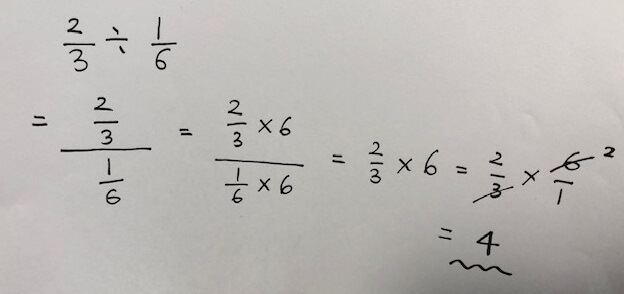
視覚的に理解するために、図解してみます。
最初のうちは、図にしやすい問題で、図を見せながら、数式をセットで示してあげるのがいいと思いました。
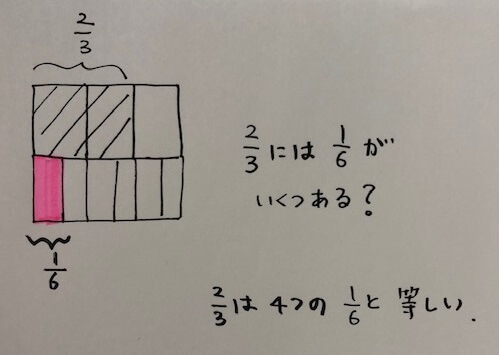
この問題もレゴブロックですっきり説明できます。
１に相当するレゴブロックを渡して、1/3、1/6を子どもに選んでもらい、じゃあ、冒頭の2/3、1/6はどうなるかな？と考えてもらうとか。
分数の概念を身につけてもらううえで、レゴブロックは使えそうです。
第３問目
次の問題も、１・２問目と同じやり方で説明できます。
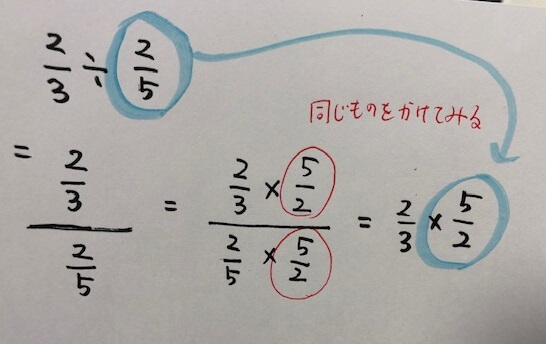
別の説明の仕方としては、それぞれに同じ数（5）をかけて導く方法もあります。
数式で示されると、まるで数のトリックですよね。
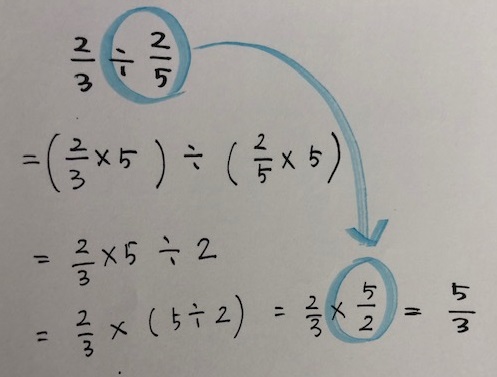
ただ、上記の数式だけでは子供がイメージできないかもしれません。
[word_balloon id=”1″ position=”L” size=”M” balloon=”talk” name_position=”under_avatar” radius=”true” avatar_border=”true” avatar_shadow=”true” balloon_shadow=”true”]イメージできることは大切だと私は思っています。[/word_balloon]
図でイメージしてもらうにはどうすれば？と考えた結果、分母を揃えてみました。
↓のように、分母を最小公倍数の15でそろえてあげて、ブロックを示してあげると、「ああ、10÷6ね」とイメージしやすくなります。
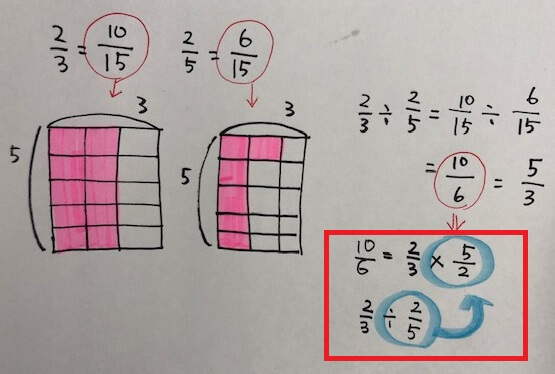
そこで、10/6を分解してみると、あれれ、逆数の5/2をかけていたのか、と納得してもらうのが狙い。
子供が「あれ、ほんとだ」と納得した様子だったら、「じゃあ、別の問題でも本当にこうなるか試してみようか」など言って、同じようにブロックを書いて一緒に考えてみるのもいいかもしれません。
ということで、別の問題でも通用するか試してみました👇
第４問目
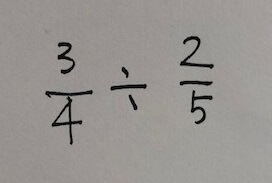
この問題を、先ほどのように、分母を最小公倍数であわせて考えてみます。
縦が4、横が5で、面積が20の四角形で考えます。
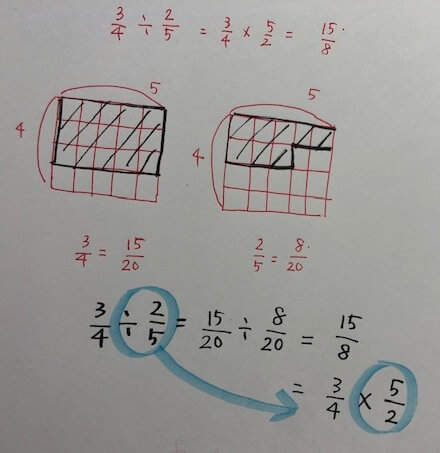
分母を20でそろえると、15÷8と導けますよね。15/8を分解すると、やはり、3/4×5/2と、逆数をかけていることがわかります。
自分でうーんうーんと考えて導いた方法（最小公倍数であわせる方法）が、一番しっくりきました。
ぜひ、親御さんも一緒になって考えてみてください！
数の遊び感覚で一緒に勉強できると楽しいですね。
いろいろな本を無料で読みたい方にはKindle unlimitedがおすすめです。
Kindle unlimitedなら初月無料で30日間読み放題です♪
こちらの記事もおすすめ
