【感想・レビュー】子どもがつまずかない教師の教え方10の「原理・原則」【親も必見】
コロナウイルスによる休校でこれからの子供の教育、一体どうすればいいのか？
頭を抱えている保護者、教育者はたくさんいると思います。
今後も断続的な休校が発生しうることを考えたとき、わたしが考えはじめたのが小学校に行かない選択です。
教育現場の混乱はこれからも数年続きますし、オンライン教育では日本は中国にとうてい及びません（詳細はこちら）。
そこで読んだのが『子どもがつまずかない教師の教え方10の「原理・原則」』。
なかなか言語化されてこなかった教え方の原理・原則が、教師だけでなく保護者にもわかりやすく書かれています。
全体的な印象は、優秀な先生は言うことが同じ！
村上先生の『人気講師が教える理系脳のつくり方』にも同じ本質が書かれていますが（感想はこちら）、育児のヒントや中学受験の裏話など対象は保護者であったのに対し、
今回の本は教師向けの本なので、より実践・理論にフォーカス。
より突っ込んで知りたい保護者にもおすすめです。
親が読むメリットとしては、
●子どものつまずきポイント・解消法がわかる
●教師・塾選びで自分の判断基準をもてる
●家庭でサポートするコツがわかる
学校や塾選び・家庭教育で、子どもにとって何がベストかを見分ける判断基準をもてると思いました。
全体を通じて印象的だったのは次の4点。
●「わかる」と「できる」の違い
●やればできる！の自信を「百ます計算」で育む
●公式・原理を音読・暗唱させる
●抽象⇒抽象の学習転移
具体的な事例とむすびつけた理論がたくさんでてきますので、目からウロコが落ちることは間違いありませんが、いちど読んだだけでは定着しないと思います。
いちど最後まで読んで、折に触れて読み返しながら、実践していくのがいいと思います。
この記事は3分で読めますので、ぜひ参考にしてください♪
目次
「わかる」と「できる」の違い
いちばん印象的だったのは、
「わかる」と「できる」を天秤にかけたうえで、
〇〇を子どもに身につけてもらうためには、どちらを優先するべきか？考えること
本ではこれを、「手続き的知識・技能の習得」と「概念的理解」は別と表現しています。
つまり、概念がわかることと、計算などができることは別ということ。
ある単元を学ぶときに、
✅概念の理解を優先させるのがいいか？
✅できるようにさせるのが先なのか？
教師が見極める必要があるということです。
わかりやすいのは、分数のわり算。
お子さんにこう聞かれたパパさん、ママさんいらっしゃるのではないでしょうか？
あーだこーだの痕跡はこちらに書いています▼
実際に、分数のわり算を学ぶ6年生の授業で、面積図を使って説明している先生が多いようです。
でも、考えてみてください。
いくら面積図を使って分数のわり算で逆数をかける理由を説明したところで、わり算の計算問題ができるようになるでしょうか？
説明を聞いて理解できる子もいる一方で、いくら説明しても理解できない子もいるはずです。
それならば、分数のやり方を教えて、繰り返し類題を解いてもらう方が学力の底上げを図れるのでは？
これが著者の主張です。
なぜなら、分数のわり算のやり方は、ほぼすべての子が身につけることができるから。
分数のわり算はこうやるんだよ、という「手続き」「やり方」を教えて、何度も反復練習すれば、確実に解けるようになります。
理数系学習塾エルカミノの村上先生も本で「分数のわり算は概念よりも小3までにマスターするべき」とおっしゃっています。
上記のことは、複合図形の面積・体積を求める場合にもいえます。
Ｌ字型や凹凸型の体積を子どもたちにグループディスカッションさせて解き方を考えさせるのではなく、学習のねらいは複合図形の体積を求めることができるようになることです。
ならば、つまずきから逆算して授業を設計する方が効果的ですよね。
このように、
子どもたちに何をマスターしてほしいか？
これを明確にしたうえで授業を設計するべきだと書かれています。
やればできる！の自信を「百ます計算」で育む
算数は1つのつまずきがほかの単元にも影響するため、
計算でつまずくとすべてでつまずく
という恐怖の連鎖があります。
本にも、
「算数でつまずいている子どもは、ほぼ例外なく計算でつまずいています」と書かれています（p36）。
かけ算・わり算ができなければ、文章問題はお手上げですよね。
しかし、自分はできないと思い込んでいる子の多くは、「自分には暗算なんて無理」「自分は九九を覚えられない」など、やろうとしないマインドセットで固まってしまっています。
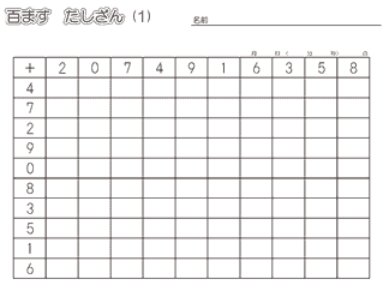
出典：ちびむす
苦手な子には二十ますからでもいいので、スモールステップでタイムを計りながら取り組んでもらいます。
百ます計算はやればやるほどタイムが縮まるので、自信につながりやすいのだそう。
しかも、はじめはみんなで音読すれば、間違えてもほかの生徒の音読で違うことも認識できます。
みんなで音読すれば、間違えて恥ずかしい気持ちもごまかすことができますね。
公式・原理を音読・暗唱させる必要性
暗唱といっても詰め込むのではなく、「思い出させる」のがポイントです。
たとえば、三角形の面積の求め方。
いっぱんに、÷2が必要な理由を、理解させることが大切だといわれていますよね。
わたしも過去に、三角形の面積の公式でなぜ÷2をするのか、自分ならどう説明するか？考えたことがあります（▼下記記事▼）
しかし、授業で理解しても翌日になると、2で割ることを忘れてしまう子がいるのは事実。
こういった子には、「わかる」よりも「できる」を優先することが大切だと著者はいいます。
そのためにできるには、公式や解法を思い出す訓練をすること。
先生：「三角形の面積はどう求める？」
生徒：「三角形の面積は、底辺×高さ÷２です」
こんな感じに。
はじめは教科書を見ながらの回答をOKとし、すこしずつ何も見ずに答えさせていきます。
これによって、公式がすぐに引き出せる記憶として定着し、学力を全体的に底上げできます。
4年生以降につまずく子が増える単位の変換も同じです。
まず、単位自体を声に出して読むことが大切。
▲を即座に読めない場合、どう読むか考えることにワーキングメモリーを消費してしまうため、概念の理解にはたどり着けません。
概念の理解の前に、まず音読することでつまずきを防ぎます。
そのうえで、
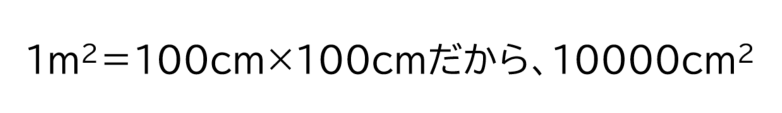
と根拠を明らかにしながら音読させるのがポイントです。
同じくつまずきの多い小数についても、繰り上がりの原理・分数を音読するのも有効な方法として紹介されています。
0.1が1個で0.1
0.1が2個で0.2
0.1が3個で0.3
・・・
0.1が10個で1
10分の1は、1を10等分した1つ分
10分の1が10個集まると1になる
などなど。
印象的だった最後のポイントは、高学年でつまずきの原因となる抽象と抽象の転移です。
抽象⇒抽象の学習転移
小学4年生以降にあるつまずきとして、
具体⇒抽象
抽象⇒抽象
の2つがあります。
このような具体⇒抽象の難しさだけでなく厄介なのが、抽象⇒抽象の転移ができないこと。
たとえばこれ▼
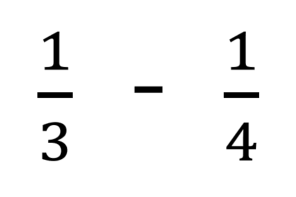
このような計算を視覚化して教えることも大切ですが、通分のやり方を教えて、できるようにさせることも大切といいます。
いちいち具体例を持ち出すのではなく、抽象を抽象のまま理解できるようにさせるということですね。
抽象⇒抽象ができるようになるには、類似の計算問題で反復練習するしかないと著者は言います。
この本は教育を学校任せにしたくない方におすすめ
この本を読むと、可視化、「できる」、「わかる」のバランス、優先度の見極めとその難しさがよくわかります。
以前のわたしは、
●算数は視覚化する方がいい
●できるだけ具体物を使うのがいい
と思っていました。
しかし、必ずしもそうではないこと、視覚化・具体例にこだわることでつまずきを誘発してしまう可能性があることがよくわかりました。
各単元でのねらいを明確にしたうえで、子どもたちができるようにするにはどう教えるのがいいか？
毎回、「ねらい」と「手立て」を見極めたうえで授業設計をしていかなければならないので先生は本当に大変です。
この本は教師向けに教える技術をわかりやすく解説した本ですが、親の立場で読んでも、
✅子どもがどこでつまずいているのか？
✅つまずきを見つけたら、どうサポートしてあげればいいのか？
十分すぎるほどのヒントがありました。
記事では取り上げられなかったポイントはまだまだたくさんあります。
先生だけでなく、学校任せにせずに子どもにベストな教育を提供してあげたいとお考えの方にも自信をもっておすすめします。
いろいろな本を無料で読みたい方にはKindle unlimitedがおすすめ。
Kindle unlimitedなら初月無料で30日間読み放題です♪
こちらの記事もおすすめ
